Mastering Finite Element Analysis: A Comprehensive Guide

Language
3201 Views
129 Enrollments
Share
Access anytime
360 Min
This course format through pre-recorded video. You can buy and watch it to learn at any time.
FREE
FREE
Why do you enroll
Key topics covered
Course details
Course tags
Course content
Why do you enroll
Unlock the power of simulation with Finite Element Method (FEM) expertise, and supercharge your career in engineering, research, and development! By mastering FEM, you'll become a sought-after professional in fields like mechanical, aerospace, civil, and biomedical engineering, with opportunities for roles like Simulation Engineer, Research Scientist, or Design Engineer. With FEM skills, you'll drive innovation, optimize designs, and solve complex problems, making you a valuable asset in industries like automotive, aerospace, and energy, and opening doors to leadership roles and entrepreneurial ventures.
Show more
Key topics covered
Types of Elements in Finite Element Method
Advantage ,Disadvantage and Application of FEM
Need of Matrix Algebra in FEM
Gauss elimination method
Direct Stiffness matrix
Global stiffness matrix
Properties of Stiffness matrix
1 D FEM for Structural Analysis
Elimination Approach
Penalty Approach
Principle of Minimum Potential Energy
Introduction to Shape Function
Shape function in Local and Natural coordinate system
Isoparametric Formulation for 1-D element
Properties of Shape Functions
Strain Displacement Matrix
Quadratic Shape Function
Steps in FEM
2 D Finite Element Method
Isoparametric Formulation Numerical
Element Stiffness Matrix
Shape function for CST element
Strain Displacement Matrix for Triangular element
Stress ,Strain Relationship Matrix
Plane Stress & Plane Strain
Gauss Quadrature Method
Weighted Residual Method
Galerkin Method
Sub Domain Method
Variational Method Introduction
Variational method Numerical by Rayleigh Ritz Method
Show more
Course Details
The Finite Element Method (FEM) is a powerful numerical technique used to solve partial differential equations (PDEs) governing physical phenomena across various engineering and scientific disciplines. This course provides a comprehensive introduction to the theory, implementation, and applications of the Finite Element Method. Topics covered include finite element discretization, interpolation functions, assembly of element equations, solution techniques, error estimation, and practical considerations in FEM analysis. Through theoretical lectures, hands-on programming exercises, and real-world applications, students will develop a solid understanding of FEM principles and gain proficiency in applying FEM to solve complex engineering problems.

Show more
Course tags
Industry domains :
Engineering Disciplines :
Course content
1
Types of Elements in Finite Element Method :
Types of Elements in Finite Element Method
2
Advantage ,Disadvantage and Application of FEM :
Advantage ,Disadvantage and Application of FEM
3
Need of Matrix Algebra in FEM :
Need of Matrix Algebra in FEM
Show more
FAQs on Mastering Finite Element Analysis: A Comprehensive Guide
Having specific question ? Ask now
Trainer’s Feedback
165 course rating
39 ratings
AF
A Fabio Riyan
2 months ago
Very useful to budding engineers
VN
VIKAS_D_ NAYAK
2 months ago
usefull
UM
URK20AE1047 MOSES
3 months ago
very useful for beginners
PS
Prathamesh Shevale
3 months ago
Excellent course.
MM
Mostafa Mohamed Elsayed
3 months ago
Good
SS
SANJAY S 22CHR058
3 months ago
Good
FK
Farhan Khan
4 months ago
Good course
MS
Marthin Siagian
4 months ago
Good Course
AA
Ayan Adhikary
4 months ago
Great 👍
AH
ABDUL HASIB HASAN ZAYED
4 months ago
Very good.
TE
Team EveryEng
5 months ago
Good
PE
Process Engineering World
5 months ago
Good
PP
Prasenjit Pandit
5 months ago
Well narrated !!
TH
Tc.Mohd Hairul Jamaludin
5 months ago
Good
TH
Tc.Mohd Hairul Jamaludin
5 months ago
Good knowledge
AJ
Anuj Jagadale
5 months ago
well prepared content.
AJ
Anuj Jagadale
5 months ago
Highly appreciable content made.
TE
Team EveryEng
5 months ago
Good course
MR
Mohammed Rizvi Uvais
6 months ago
Well prepared presentation
MA
Mario Alberto Aguilar Herrera
7 months ago
Simple but excellent explaining
SC
SARTHAK CHAVAN
9 months ago
The lecture was quite good and interesting
HN
Harishankar Nagapuri
9 months ago
Excellent
SN
Shripad Nilakhe
10 months ago
Nice
NG
Nishanth G
10 months ago
Good Seminar
D2
DAVE 2D
10 months ago
Good session and explain as i expected
SK
Srinivasulu Killa
10 months ago
Good
bm
bhavin mehta
a year ago
Excellent course.
SA
Syed Aamir
a year ago
Good
SG
Sampath G
3 months ago
nicely explained
MY
MUHAMMAD YOUSUF KHAN
6 months ago
good good
PK
Prasanna Koduru
7 months ago
Good
SG
Sampath G
3 months ago
Should have discussed ddetails like 1.why density based solver. 2.why pressure boundary conditions. 3.How pressure values affect the working of nozzle etc
MF
Mustahid Fahim
3 months ago
Lectures are good but it's already available in the YouTube nptel lectures why should I watch here
KM
Khushal Mahajan
3 months ago
Why uploading NPTEL videos on your site ?
NA
Noor Alam
6 months ago
Good
YD
Yogesh Desai
a month ago
Useless
JK
Jahanzeb Khan
5 months ago
where are the other video
rk
recheal komugisa
7 months ago
Request for the video
TK
TANMAY KULAYE
10 months ago
Only one video is uploaded, rest of the videos are not there. 👎👎👎 Please upload other videos of Green Hydrogen.
Certificate of Mastery

Receive well recognised certificate that you can showcase on
Featured courses
Hazard Identification and Risk Assessmen...

How to prevent corrosion in the oil and ...

Application and use of "Green Hydrogen"

Career in EPC projects for Freshers

Career in EPC Cost Estimation

Learn MATLAB Programming

More Technical Courses From Team EveryEng
Pressure Vessel Essentials: Need of code...

How to prevent corrosion in the oil and ...

Application and use of "Green Hydrogen"

Gas Turbines with special emphasis on hy...

Career in EPC projects for Freshers

Career in EPC Cost Estimation

Bolt Torque Calculations using Dennis Mo...

Introduction to SAP and its role in the ...

More Articles From Team EveryEng
Davisson and Germer Experiment

Compton Scattering Effect

Coherent Source

Black Body Radiation

The engineering services is changing and...

What is first, YOU or YOUR COUNTRY?

Visionary Leaders make the nation great

Engineers need business acumen to be suc...

Collaboration is the first step of intel...

More Communities From Team EveryEng
Similar Content Learn:
Basic of CMS IntelliCAD and GD&T

Fundamentals of Quality, QMS & ISO-9001

Buffer Tank - Basic, Concept, Design, Ca...

Business Excellence through Quality, QMS...

Renewable Energy, Energy Storage Systems...

Similar Content Mentor:
All About Interviews

How to motivate & encourage team bonding...

Time Management essentials for Engineers...

COMMUNICATE TO WIN - The most important ...

Similar Content Seminar:
The Petrochemical and Refining Congress:...
The Oil and Gas Decarbonisation Congress...
OIL & GAS AUTOMATION AND DIGITALISATION ...

7th International Oil & Gas Chemistry, C...

Similar Content Blogs:
Reaching Net-Zero: The Power of Predicti...
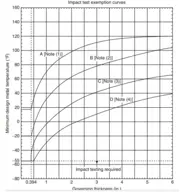
Technical Basis for Impact Test Exemptio...

A brief mathematical overview of the for...

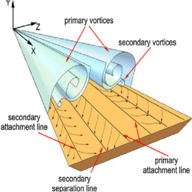
Aerodynamic physics of the Delta Wing

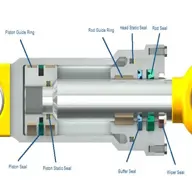
Seal of Hydraulic cylinder.

PRC Europe 2025: Italian Partners at the...
Similar Content Community:
Firefighting Design By Naga

Engineer's Corner

Cathodic protection

Corrosion

Similar Profile:

Vijay Sachdev
Consultant - Project & Pr...

Debojyoti sen
MD & CEO, SAURYAJYOTI REN...

Sabari Kuppuraj
Engineer

Dr Bhawani Singh Rathore
Renewable Energy Coach an...

Mir Abbas
Senior Engineer

HEXSPUR FOUNDATION
Mechanical Design Enginee...

Anup Kumar Dey
Owner of https://whatispi...

Please wait